[最も人気のある!] e^2x 微分 970072-E^2x+3 微分
In this video, we will learn to integrate exponential of 2xOther topics for this video areExponential of 2xIntegral of e^2xIntegration of e^2xAntideriv單元 26 指數函數的微分 ({ §54) 欲}析ÖNbƒbDúbƒbíbç模型, Ûê l NbƒbDúbƒbíûƒbíd† íl, Nbƒbí }d† AÍNbíûƒbÑ d dx (ex) = ex I f(x) = ex 根Wûƒbíì2, Nb J£ "Ìí4", f0(x) = lim h→0 f(x h) − f(x) h = lim h→0 exh − ex h = lim h→0 ex(eh − 1) h = ex lim h→0 eh − 1 h (1) QO微積分I 14 25 9 対数関数の微分 関数y = ex は定義域がR,像がR = (0;1) である単調増加関数であっ たからその逆関数を考えることができる.x に対し,y はex と定まるのだか ら,このy に対応するx はloge y であることは対数の定義から自明なことで ある.すなわち,x とy は方程式y = ex を満たす
如何使用参数变化求解y Y 2y E 3x 教育小本子
E^2x+3 微分
E^2x+3 微分-其特征方程为:r^24r4=0 ,r1=r2=2 齐次线性微分方程的通解为:Y=(C1C2x)e^2x 因为λ=2不是特征方程的双根,所以应设y*=(b0xb1)e · 対数微分法を用いた例題 次の関数を微分せよ。 〈解答〉 パッと見た感じ、logを使うようには見えないんだけど 今回の関数を微分するためには対数微分法というやり方を用います。 まずは、底 とする対数を両辺にとります。 ここから両辺を微分すると




高校数学 グラフのかき方 1 問題編 映像授業のtry It トライイット
0721 · >> ^2e^2x 基本求导公式(e^x)'=e^x得到(e^2x)'=e^2x*(2x)'=2e^2x把2x设为变量U,对e^u求导得e^u(即e的2x方),对u求导的2;两者相乘得2倍e的2x方 n的倒数*e的n次方2*e的2x次方e的n次方倒数e的2x次方的导数是2e的2x次方如果它是一个导数值那原函数是1/ 扩展资料任何非零数的0次方都等于1原因如下 通常代表3次方5的指数関数の微分 指数関数の微分は、べき関数\(y=x^n\)とは異なり、\(y=2^x\)のように指数が変数である関数の微分を考えます。 基本的に数Ⅲでは\(e^x\)の登場回数が多いですが、もちろん\(2^x\)などの関数も出番がないわけではありません。微分方程式y'+2y=3xを解くとどうなりますか? 回答数 2 件 Akito Sawamura , データ分析・コンサル 回答日時 10 カ月前 · 執筆者は5,464件の回答を行い、953万回閲覧されています y' e^ (2x)2y e^ (2x)=3x e^ (2x) (d/dx) (y e^ (2x))=3x e^ (2x) 積分して y=e^ (2x) ( (3/4)e^ (2x
積の微分公式です。 数学IIIで習います。 重要度★★★ 10. { f ( x) g ( x) } ′ = f ′ ( x) g ( x) f ( x) g ′ ( x) もっと詳しく: 積の微分公式の頻出問題6問 積の微分公式を使ったいろいろな微分公式です。 重要度★☆☆ 11. ( x e x) ′ = e x x e x 12. ( x sin0211 · e的2x次方的微分是:2 (e^2x) 微分由函数B=f (A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。 当自变量X改变为X X时,相应地函数值由f (X)改变为f (X X),如果存在一个与 X无关的常数A。 · e^2x を微分すると、 (2)* (e^2x)となるので、 e^2x の積分は、 (1/2)* (e^2x)と判明します。 79
逆微分演算子 微分演算子 \(D\) は, \(\displaystyle \frac{d}{dx}\) から敢えて書き換えることで何か良いことがあるのでしょうか? 実のところ,これだけでは微分演算子の有り難味が私には分かりません。ところが,逆演算子を考えることで,とても便利なツールになってきます。 · eの偏微分 0115 e^ (x^2)2xy (y^2)をxとyで二階微分します。 一階微分の fx=(2x+2y)e^ (x^2)2xy (y^2)まではいいのですが、 fxx=2{2((x+y)^2)+1}e^ (x^2)2xy (y^2)の意味がまったくわかりません。 +1って何なのですか? 同じことをもう一回する · 指数関数y=a^xの微分公式の4通りの証明 y'=a^x\log a y′ = ax loga である。 上記公式を4通りの方法で証明します! 指数関数の取り扱い,極限操作の練習にどうぞ。 e e であることを表します。 底が a a のときは明記します。




求微分方程的通解y Ytanx Sin2x的疑问 雨露学习互助




如何画出函数y E 2x 的图像 百度经验
Simplify e^ (2x)*e^ (2x) e2x ⋅ e2x e 2 x ⋅ e 2 x Use the power rule aman = amn a m a n = a m n to combine exponents e2x2x e 2 x 2 x Add 2x 2 x and 2x 2 xE 2 は定数なので,積の微分公式を使う必要はありません。e x だけ微分すると, y'=e 2 ×(e x)'=e 2 ×e x =e x2 と答えが求まります。微分 e ^ x (ex)′ = ex ( e x) ′ = e x 導出 (ex)′ = lim Δx→0 exΔx−ex Δx ( e x) ′ = lim Δ x → 0 e x Δ x − e x Δ x = lim Δx→0 ex(eΔx−1) Δx = lim Δ x → 0 e x ( e Δ x − 1) Δ x = ex{ lim Δx→0 eΔx−1 Δx } =




Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム



E 2x の微分が2e 2x になる理由を教えてください Yahoo 知恵袋
積分 {e^ (2x)}sinx ∫ e2xsinxdx ∫ e 2 x sin x d x の積分を 部分積分法 を用いて計算する. ∫ e2xsinxdx = ∫ (1 2e2x)′ sinxdx = 1 2e2xsinx−∫ 1 2e2x(sinx)′dx = 1 2e2xsinx−∫ 1 2e2xcosxdx = 1 2e2xsinx− 1 2 ∫ e2xcosxdx ・・・・・・(1) ∫ e 2 x sin x d x = ∫ ( 1 2 e 2 x) ′ sin x d x = 1 2 e 2 x sin x − ∫ 1 2 e 2 x ( sin x) ′ d x = 1 2 e 2 x sin x − ∫ 1 2 e 2 x cos x d x = 1 2 e 2 x即该方程的齐次微分方程的通解为: y*=c1sinxc2cosx 又因为λiw=22i,不是特征方程的根,则设特解为: y1=(msin2xncos2x)e^2x; · でも、微分するとき、まとめてxと置いた部分を後ろに微分してかけます。 ですから、 e^ (2x)は2xの部分をまとめて考え 5 5 1759




全导数例题




高校数学 グラフのかき方 1 問題編 映像授業のtry It トライイット
今回は,指数関数y=e x の微分公式について解説します。指数関数は,aを定数としてy=a x で表される関数ですね。この指数関数の中でも,特に底a=eの場合の微分公式について学習していきましょう。0710 · 関数f(x)=e^2xを=0で2次の項までテイラー展開しなさい。また、その結果を用いてe^02の近似値を算出しなさい。f(0)=e⁰=f(a) 微分の公式の導き方 8 微分可能なのに導関数が不連続? 9 積分の問題。微分とは、わかりやすくいえば、関数のグラフの傾きを求めるものである。 関数のグラフの傾きは、y=f(x)において、 1.二次関数 y=ax 2 +bx+c について微分をしてみる。 2 2 2 +bx+c) =ax 2 2 2 -bx-c 2 2 2.三角関数 y=sinxを微分してみる。
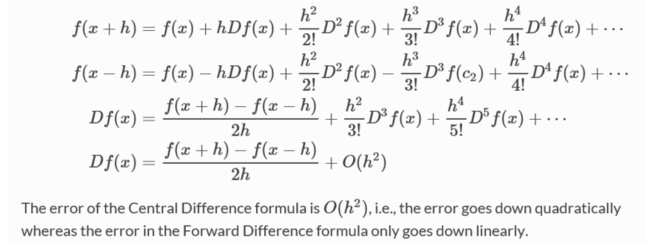



如何计算微分 Weixin 的博客 Csdn博客
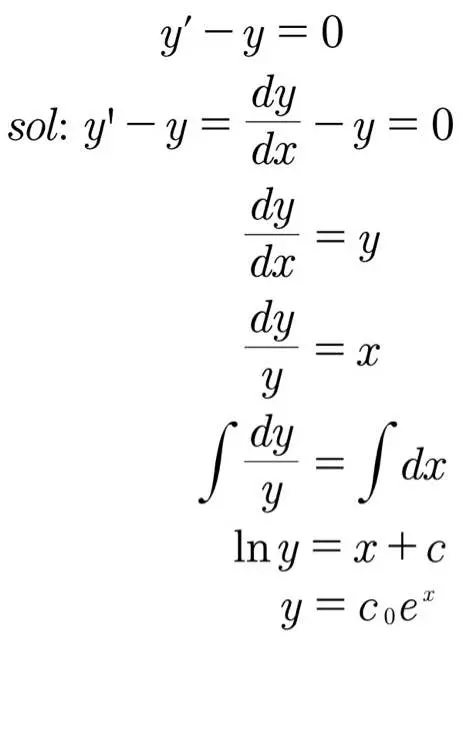



科普 简单常微分方程的解法 哔哩哔哩
00 · 基本的には、eのx乗を微分した場合のそのままeのx乗となる性質を活用していきます。 ・微分の場合 すると (e^2x)の微分=(e^2x)' = (2x)' (e^2x) =2e^2x と計算できました。2x乗の係数が微分により前に出てくることに気を付けるといいです。 ・積分の場合0721 · 名前 * メール * サイト 次回のコメントで使用するためブラウザーに自分の名前、メールアドレス、サイトを保存する。次の式 y''P(x)y'Q(x)y=0 を「2階線形同次微分方程式」というのに対して, y''P(x)y'Q(x)y=R(x) を「2階線形非同次微分方程式」といいます. 定数係数の2階線形微分方程式については,同次方程式は次の(1)の形,非同次方程式は(2)の形になります.( a, b は定数の係数)



微分方程y 4y E 2x的通解为 数学竞赛平台 数学帮 Math110
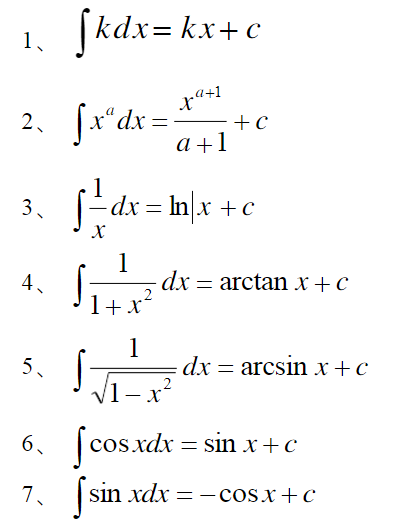



单变量微积分笔记11 微分和不定积分 我是8位的 博客园
微分する関数を入力してください。 変数 微分階数 1 2 3 4 5 6 7 8 9 微分電卓 は、解析的微分を用いて、指定された変数について関数の導関数を計算します。 10次 までの導関数がサポートされています。 微分電卓は、関数とその導関数のグラフを描画することができます。 数式の書式を表示2405 · 微分演算子Dを使って、(D²2D2)y=e^(2x) ここで、f(D)=D²2D2 と書くと f(D)y=e^(2x) になる。 右辺が、e^(αx) の形の場合は、特殊解は、微分の公式一覧 このページでは、関数 f (x) f ( x) を 微分 して得られる導関数 f ′(x) f ′ ( x) の基本的な公式を掲載しています。 また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。 導出方法はみなさん自身でご確認の上
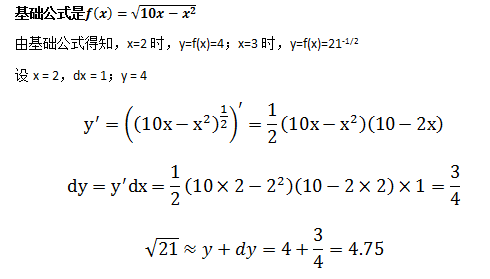



单变量微积分笔记11 微分和不定积分 我是8位的 博客园




科普 简单常微分方程的解法 哔哩哔哩
1219 · Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooE^2x的导数是怎么算出来的 用复合函数求导公式f'(g(x))=g'(x)*f'(g) e^2x中,f(x)=e^x,g(x)=2x 因此根据复合函数求导公式,f'(g(x))=(2x)'*(e^2x)'=2*(e^2x) e的2x次方原函数是什么 ∫e^(2x)dx=05e^(2x)C,C为任意常数所以原函数为05e^(2x)C e^2x的偏导数是什么?求y=e^2x/x^2的微分 求y=sin (e^2x)的微分y' 求微分 (1)y=x^2 e^2x 求y=e^2x乘以cos3x的微分 y=x^2乘以e^2x的微分,




Arcsin E 2x 的微分求解 數學板 Dcard
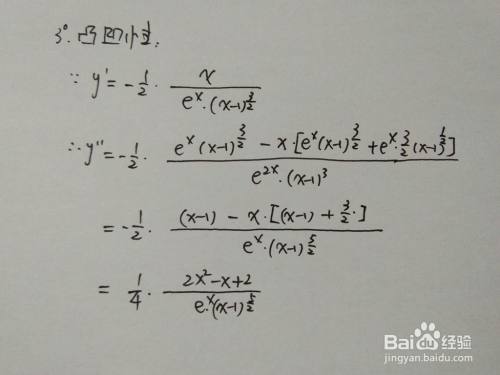



函数y 1 X 1 E 2x 的图像示意图 百度经验
· また微分方程式です汗 y'=e^2xye^x なんですが、タイプは dy/dx=p(x)yq(x) 型の「線型方程式」らしいです。 この線型方程式の一般解法が両辺にexp(∫p(x)dx)を掛けるというものらしいのですが、 この使い方を分指数関数 == 指数関数 (2) == 指数関数のグラフ y=2 x , y=3 x などのように指数の部分が変数になっているものを指数関数という. y=a x は a を底とする指数関数と呼ばれる. y=2 x のグラフは右 図1 のようになる. また, y=3 x のグラフは右 図2 のようになる0305 · 0503 問題 微分 積 合成関数 指数関数 音声解説 Twitterでシェアする 公開記事一覧 RSS/Atom 結城浩(ゆうき・ひろし) / Hiroshi Yuki @hyuki




The Derivative Of E 2x Derivativeit




Y等于x的2x次方的微分 搜狗搜索
· 不定積分 ∫ 4 x 2 e 2 x d x \int 4x^2 e^{2x} dx ∫ 4 x 2 e 2 x d x を求めよ。 この場合も同様に,多項式 4 x 2 4x^2 4 x 2 の側を微分します。 ただし2回部分積分をする必要があります。 · e^(ikx)の微分って、ike^(ikx)でいいのでしょうか?(i虚数、k定数、e:ネイピア数) それとも虚数のところで特別な処理が必要なのでしょうか。 / 合ってるんじゃないでしょうか。 u = kxとおいた場合、du/dx = k e^(iu) = cos u i sin uなので d/du(e^iu) = d/du(3007 · (e^2xやe^3xなど) 結論からいいますと、e^axを微分した場合にはae^axとなります。 これは(e^ax)'=(ax)'(e^ax)= ae^ax という流れの計算になるためです。




实验七用mathematica解常微分方程



E 2xの微分は E 2xの微分ってなんですか Yahoo 知恵袋




微分方程y 3y 2y X 2 E 2x 的特解形式是什么 知乎




1 计算 Lnx X 2dx 其中x 1 E 雨露学习互助



如何使用参数变化求解y Y 2y E 3x 教育小本子




高阶微分方程 Jason S Blog




2 6 Chain Rule Example 1 E 2x Youtube



微分方程xy E 2x Y 求y 作业 慧海网



E 2x 積分 達人專欄 Uvyo
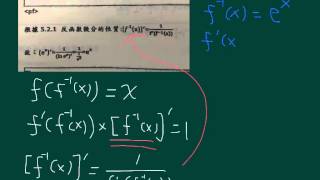



E X的微分證明法 Youtube
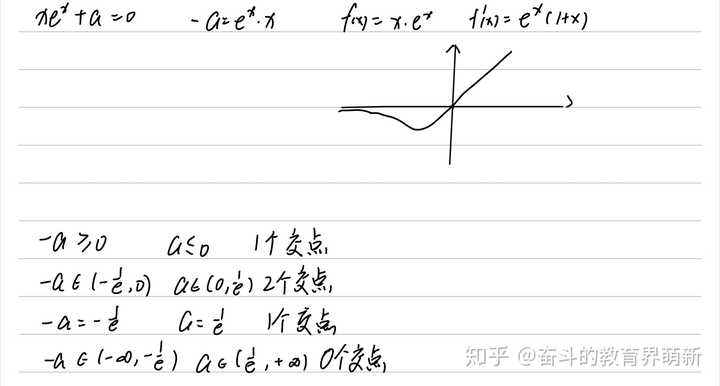



Xe的 X次方的原函数 Xsinx的原函数 Xe 2x原函数计算过程




E的负2x次方积分 在线图书馆




第二章函数微分学 2 3 函数的微分本节内容一 微分的定义二 微分的几何意义三 微分公式与运算法则 Ppt Download




Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム



Y E 2x 2の微分 Y E 2x 2 y Eの 2x乗のxの二乗 Yahoo 知恵袋




想請問直接對 2x 作微分這樣是對的嗎還是一定只能對未知數做微分 Clear



已知y1 E 3x Xe 2x Y2 E X Xe 2x Y3 Xe 2x是某二阶常系数非齐次线性微分方程的3个解 则该方程满足y 0 0 Y 0 1的解为 数学竞赛平台



E的2x次方 万图壁纸网




指数函数 维基百科 自由的百科全书



求下列各微分方程满足所给初始条件的特解 3 Y 10y 9y E 2x Y X 0 6 7 Y X 0 33 7 数学竞赛平台 数学帮 Math110



设f X 在 0 内连续 且lim X F X 1 证明函数y E Xs X 0 E F T Dt满足微分方程dy Dx Y F X 并求ilim X Y X 数学竞赛平台
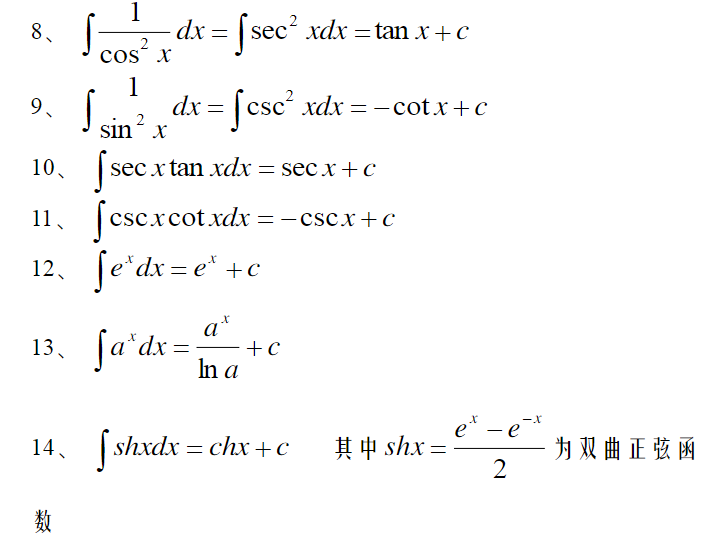



单变量微积分笔记11 微分和不定积分 我是8位的 博客园



指數e 微分 看線圖輕鬆賺外匯




Nmt Tutorial 3扩展b 自动微分 Tingxun S Blog




如何画出函数y E 2x 的图像 百度经验




求解常微分方程dc T Dt E T V Lc T E T 当做已知的方程 把c T 的表达式求出来 雨露学习互助



求微分方程的通解y 5y 6y Xe 2x 数学作业 解题作业帮



高校数学の微分です Y Xe 2xの凹凸を調べ 変曲点を出す問題な Yahoo 知恵袋




自然對數 维基百科 自由的百科全书



隐微分法




自然對數 维基百科 自由的百科全书
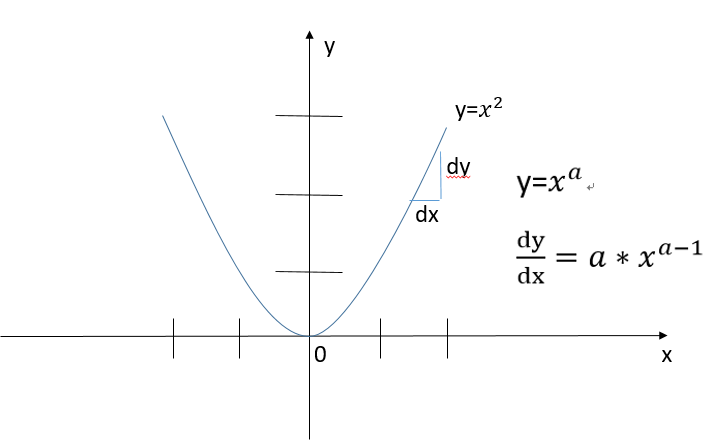



微積分概述 大家一開始在學微積分時應該都是從背公式開始的 首先簡介一下微分 通常老師在介紹時 By Judy Chen Medium




最美的公式 你也能懂的麦克斯韦方程组 微分篇



E 2xの微分は E 2xの微分ってなんですか Yahoo 知恵袋
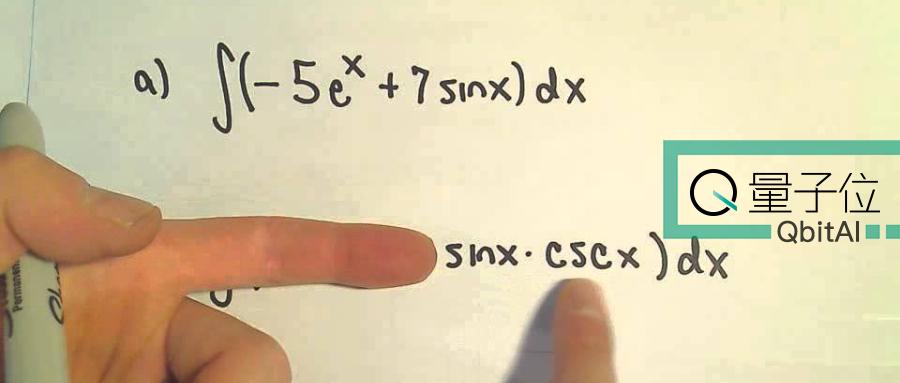



Ai拿下高数一血 求解微分方程 不定积分只需1秒 成绩远超matlab 知乎




高数微分习题求下列各函数的微分dy 1 Y 3x 2 Ln 1 X 2 Y E X Cosx设由下列方程确定y是x的函 雨露学习互助




E Axを微分すると何 E 2xやe 3xなど E Ax B Y E 2x 1など を微分するとどう Ae Bxを微分するとどうなるか ウルトラフリーダム



求以下列各式所表示的函数为通解的微分方程 2 Y C 1 E C 2 E 2x 其中c 1 C 2 为任意常数 数学竞赛平台 数学帮 Math110



已知y1 E 3x Xe 2x Y2 E X Xe 2x Y3 Xe 2x是某二阶常系数非齐次线性微分方程的3个解 则该方程满足y 0 0 Y 0 1的解为 数学竞赛平台




1 第六章单变量微分学郇中丹学年第一学期 2 基本内容 0 微积分的创立 1 导数和微分的定义 2 求导规则 3 区间上的可导函数




待定法求微分方程的解 微分 方程y 39 39 2y 39 X 2 E 2x 1用待定系数法确定的特解形式是 具 三人行教育网 Www 3rxing Org




E的负2x次方积分 在线图书馆



高等数学视频第七十一讲 精选 其他类型的常微分方程 内容包括可直接积分的微分 方程 需要进行变量替换再进行求解的方程 讲解详细 条理清晰 动画演示 通俗易懂 哔哩哔哩




E的负2x次方积分 在线图书馆



1



E的2x次方的导数 搜狗图片搜索
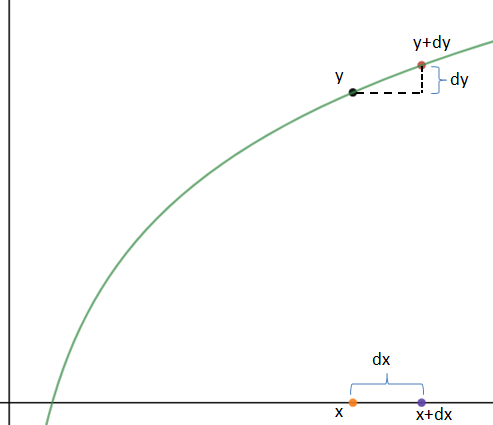



单变量微积分笔记11 微分和不定积分 我是8位的 博客园




求由方程e的xy次方 2x Y的3次方所确定的隐函数y F X 的微分dy 雨露学习互助




E的2x 1 次方怎么分解 搜狗搜索




微博搜索
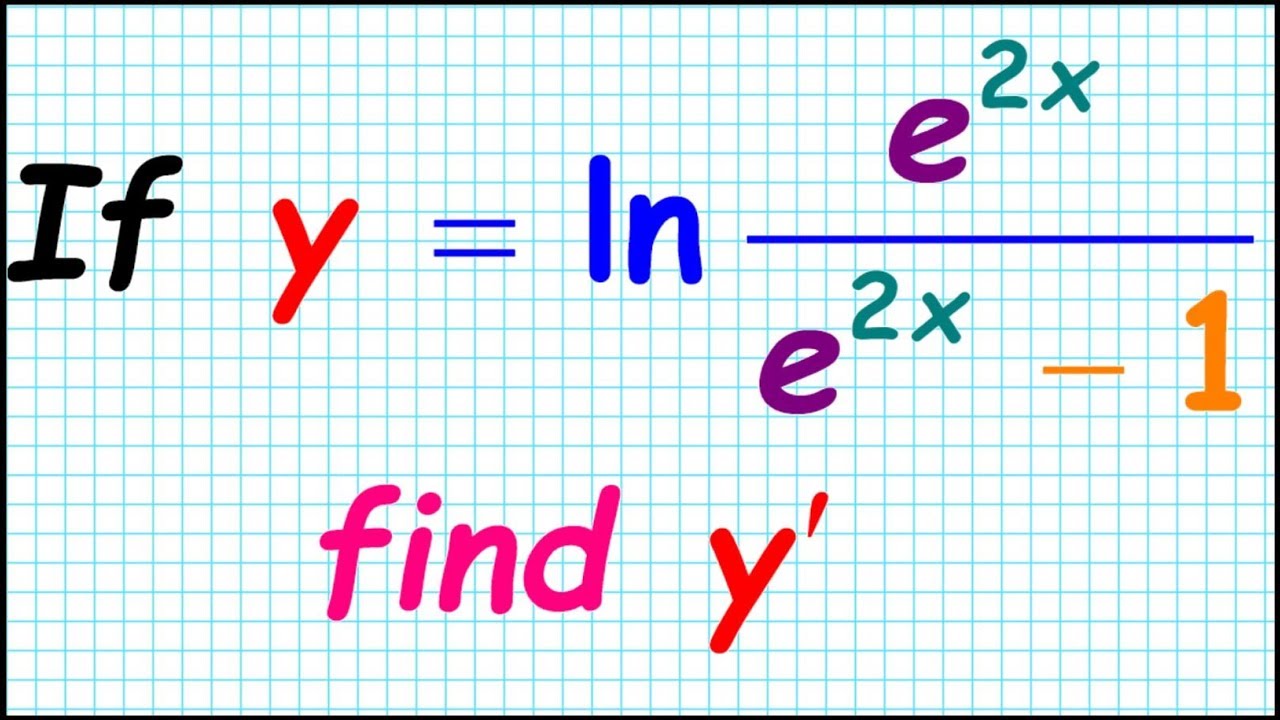



How To Differentiate Ln E 2x E X 1 Derivative Differentiation Collection Chain Rule Cr9 Ap Calc Youtube



E的2x次方 万图壁纸网




利用像函数的微分性 求教利用象函数的微分性质 求f X T E 三人行教育网 Www 3rxing Org



已知y 1 Xe X E 2x Y 2 Xe X E X Y 3 Xe X E 2x E X是某二阶线性非齐次微分方程的三个解 求此微分 方程数学竞赛平台



3
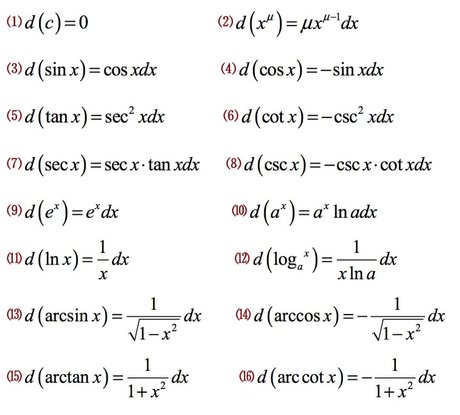



数学公式 360图片




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube




E的2x次方的微分是什么 E X 2微分




E 2x 積分 達人專欄 Uvyo




Ppt 5 3 指數函數的導數powerpoint Presentation Free Download Id
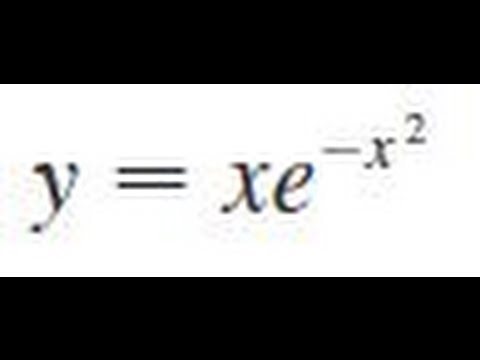



Y Xe X 2 Find The Derivative Of The Function Youtube




常微分方程 知乎




指数函数 维基百科 自由的百科全书



如何解决 数学 Y 4y 5y E 2x Cos X 教育小本子




一个求导的例子 知乎




如何计算微分 Weixin 的博客 Csdn博客



如何使用参数变化求解y Y 2y E 3x 教育小本子




一阶微分方程 Jason S Blog




請問第三小題為何e 2x 1 會等於2e X 1呢 Clear




2 5函数的微分 早做准备




导数法则



Alevel数学题型 隐函数求微分题解题技巧解析 A加未来国际教育
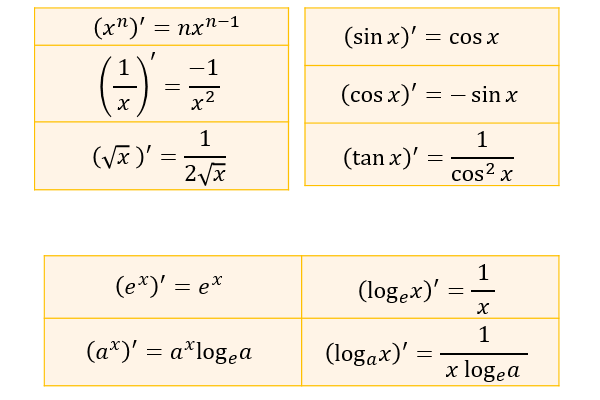



微分の公式一覧 アタリマエ



E的2x次方 万图壁纸网
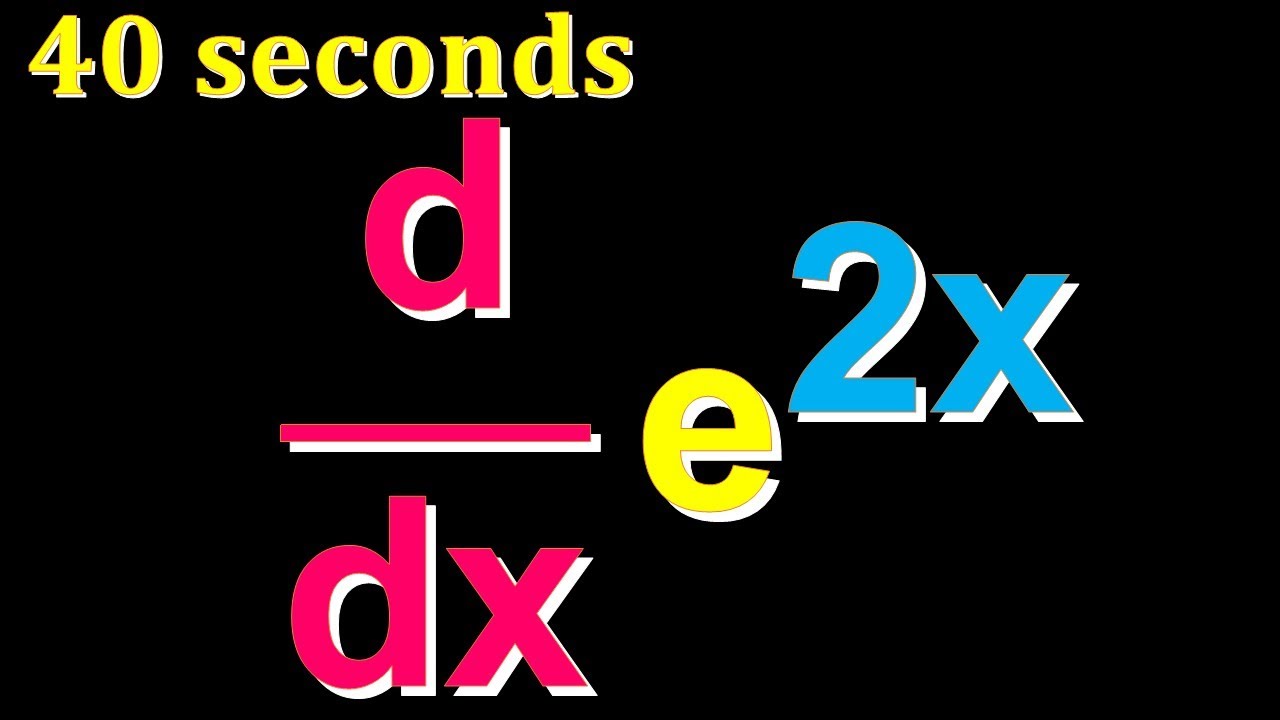



Derivative E 2x In 40 Seconds Derivative Of E 3x In The Description Youtube




已知y1 Xe X E 2x Y2 Xe X E X Y3 E 2x E X Xe X 是某二阶常系数非奇次线性微分 雨露学习互助




数学 导出复杂函数 函数y 根数 E 2x 1 被导出 365bet送彩金 365注单审核不能提款




までお願いします Clear




微博搜索




Ppt 指數函數的導數powerpoint Presentation Free Download Id




1 E 2x 2e X Dxがわかりません T E Xと置きました 答えは1番 高校 教えて Goo




指数函数 维基百科 自由的百科全书




電腦王阿達 轉 幹 看不懂qq 數學不會背叛你不會就是不會好東西 Www Kocpc Com Tw Archives Facebook



E的2x次方 万图壁纸网




E2x积分 E的2x次方的不定积分是多少 三人行教育网 Www 3rxing Org




等式两边全微分 Z E 2x 3z 2y 对等式两边求全微分怎么做 三人行教育网 Www 3rxing Org


コメント
コメントを投稿